
Okay, I did run quickly past one issue: given two points $A$ and $B$ on the circumference, there are two points at a distance $r$ from both of them. Given the above constraints on $x$, the radius $r$ lies within this interval. The maximum length of $CA$ is unbounded, so we can say that its length is on the interval $[x, \infty)$. This length-call it $x$ is anywhere from 0 (if $A$ and $B$ also coincide) to $r$ (if $AB$ is a diameter of the circle).
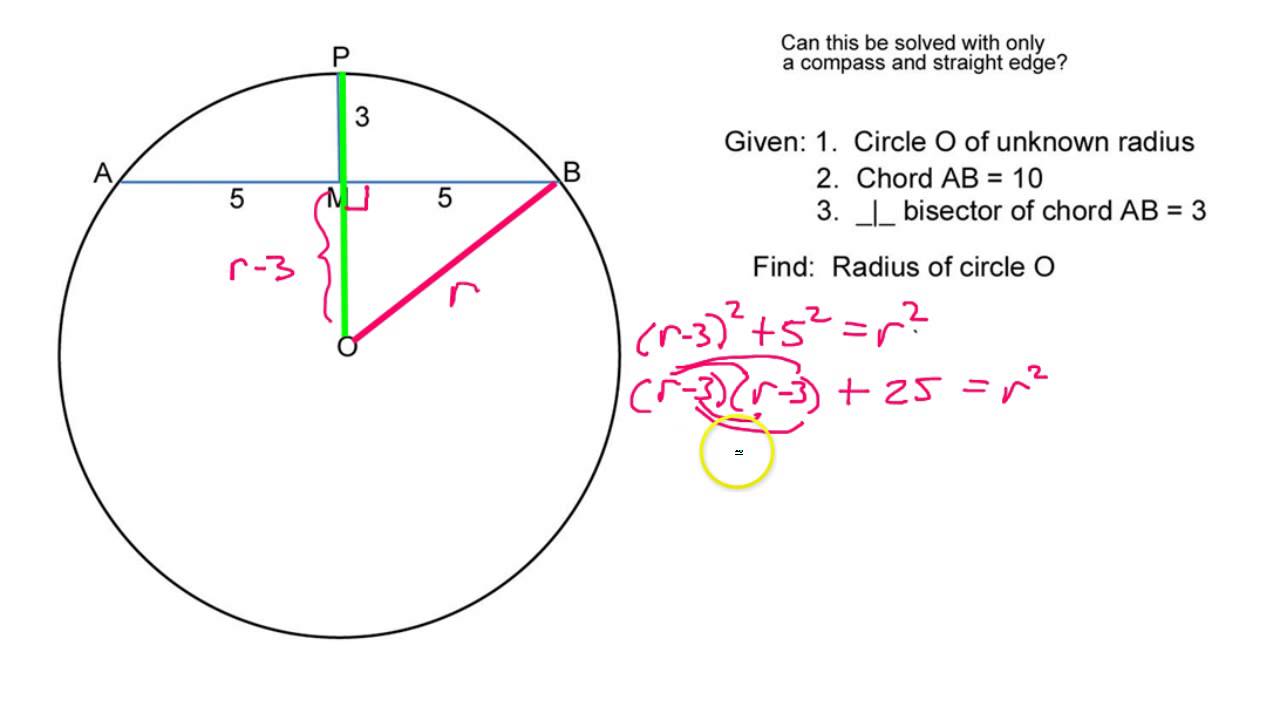
The minimum length of $CA$ is in the degenerate case where $C$ and $D$ coincide. By the above lemma, this requires that the radius be a possible length for the line segments $CA$ and $CB$. It is necessary now to prove that the circle’s centre is also on this locus, and hence is a possible location for $C$. Point $C$ is an arbitrary point on this locus. What they’ve actually proven is that the perpendicular bisector is the locus of points equidistant from $A$ and $B$.

I’ll use this lemma below to complete the proof. Perhaps what they meant to say is that the centre is the unique point at a distance $r$, the radius, from any two points on the circumference. In fact every point within a circle lies an equal distance from some two points on the circumference! As Doug M said in a comment, the last statement of the “proof” in the question is false: “equal distance from two points on the circumference” is not a unique property of the circle’s centre.


 0 kommentar(er)
0 kommentar(er)
